


Ask an Engineer Why and How, Installment 6: Why aren’t roads flat?
Friday, May 31, 2019
Four or five years ago I was asked by Kristen to put together an engineering exhibit to teach junior high students about highway design. I thought about it and came up with a topic pretty quickly – Why Aren’t Roads Flat? We had just completed the design of a fairly complex roadway on a steep curvy hill, and different engineering teams in our office were challenged to develop a design that preserved trees, kept existing driveways, would drain when it rained (without eroding a stream and ditches), was not too steep, and would be safe when it was icy. Critically important issues were that it had to fit within the existing right of way and the project had a very constrained budget. These are typical concerns, but this one was difficult, and you would never guess it if you saw the road – because the design works. I still smile when I drive that curvy stretch of road – especially when I’m piloting my “fun” car maybe a few mph above the posted limit…
So, I went to the toy store, bought some Hot Wheels cars, some track, a speed sensor and a rubber band powered car launcher. I mounted a couple exhibits on a board, made some labels, gave the exhibit a name, and it was a hit with the kids! Because I would be the presenter only the first time it was to be used (with assistance from Kristen), to work out the kinks, I had to develop a brief write-up so that anyone could give the presentation. Several years and job fairs later it is still a big hit, and I just used it again a 5½ weeks ago at Brooks Middle School in Bolingbrook– I wish that I could get as many smiles from my real work.
Here is the instruction booklet:
Model Car Super-Elevated Test Track (McSETT)
The purpose of the Model Car Super-Elevated Test Track (McSETT) is to expose students to the physical properties of the surface profiles of our roadways with a simple question,
“Are roads flat?”
The answer is “No.”
The Engineer then asks the students another question, to which a complete answer is seldom given, “What moves on roads?"
The typical answers are, “Cars. Trucks. Buses. People. Raccoons, but not fast enough, then they stop moving…” but the seldom provided answer is “water”.
The McSETT has displays that allow the Engineer to explain to the students how we design roads so that water doesn’t puddle on the pavement through the concepts of “crown”, “cross-pitch”, and “vertical curves.” The topics of “friction factor”, “design speed” and “design vehicle” can also be discussed as we present the balance between keeping roads both safe and dry in all seasons and how a “wet” road can become unsafe.
I need to step in here and briefly explain a few of these topics to you.
The way that I present this can be lengthy or short depending upon the interest and responsiveness of the students. I’m doing my best to give you the short version here, but I’ve added some of the physics and math just to show you a hint of the complexities that are involved in a “simple” roadway design.
We put a “crown” (the center of the road is higher than the edges) on low-speed roadways to push water to the sides where it is collected in the side ditches or curbs and storm sewers. Most local roads are built this way.

We use a “cross-pitch” (one edge higher than the other) to push all of the water to one side. Most highways are built this way.
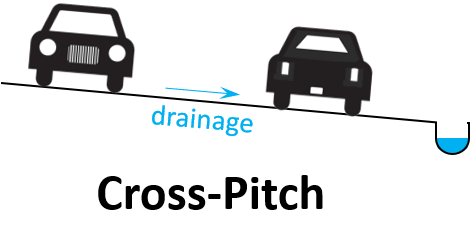
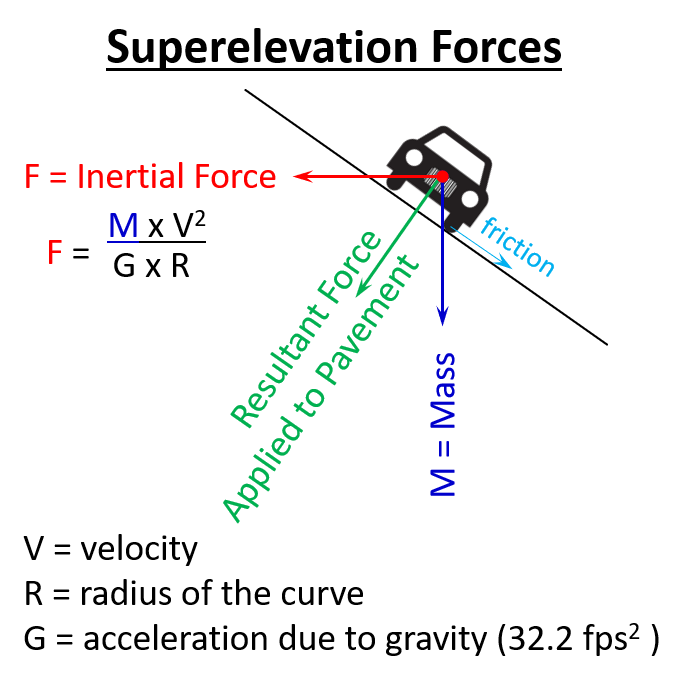
We also use a cross-pitch on high-speed or abrupt curves, but in a curve we call it “superelevation”. We apply superelevation to help vehicles “stick” to the pavement when going around curves. For my physicist friends this is over-simplified, but as a car travels along a curve its inertia makes the car try to fly off the back of the curve. We sense that there is a force (centrifugal force) that is pulling the car off of the curve and pulling the driver to the left or right (depending upon the direction of the curve). In reality it’s not a force, but it is the inertia of the car and its contents

trying to move in the direction that they were going before you turned the steering wheel. To further confuse you about this “non-force”, we call that inertia “F”.
This inertia is proportional to the weight of the car times the velocity of the car squared divided by the radius of the curve. So, when all other terms in the equation remain unchanged:
- a lighter car is more “nimble” and grabs the curve better (less M means less F)*;
- it is harder to keep a car steady on a short radius curve, than a long radius curve (less R means more F);
- the faster you drive, the stronger the inertia is trying to pull you off the curve, squared (higher V means more F2); and
- it’s more difficult to drive on the Moon than on Earth. (the G factor in the equation is the effect of gravity, less G means higher F).
* There is a balance. Although F is less for a light vehicle than for a heavy vehicle, a light vehicle puts less force on the tires and therefore less friction is produced in direct response to F. So, the fastest vehicle around a given curve won’t be the lightest, or the heaviest – it will be somewhere between.
On flat pavement, the only way to counter this inertia is by the friction of the tires and by accelerating the car “through” the curve. It’s a trick I learned from a professional driver when I was a teenager, and once I understood the mathematics and the physics, it made perfect sense. When you accelerate a body it creates a force, and that force is equal to the mass of the object times its rate of acceleration (f = M x a, Newton’s Second Law of Motion). So, when you accelerate (a) your car with mass (M) through the curve you are creating a force (f) in line with the curve, because that is where your tires (and the car) are pointed. This force is perpendicular to the centrifugal inertia, so you can never accelerate enough to fully eliminate it, but the resultant
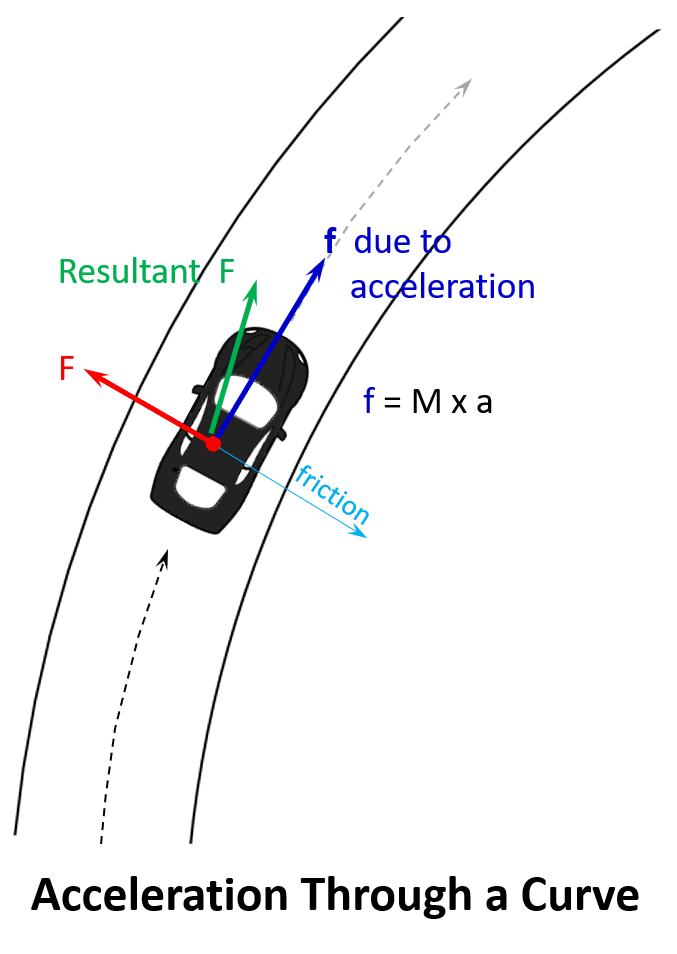
force is more in line with the curve, and easier for the friction of the tires to overcome.
Another trick I learned was from an experienced driver on a road course. You hit your brakes as you come into a curve. This pushes the weight of the vehicle down and to the front, and increases the friction from your front tires, which are turned in the direction of the curve. Road courses have curves that are essentially flat – so the rhythm is to accelerate in the straights, brake at the “brake point” into the curve, accelerate through the curve and set yourself up for the next curve. Key to every curve is “establishing your line” to reduce the radius of the curve. The whole experience is centered around reducing F – this lets you go faster and allows your tires to last longer. I like to pretend that I’m a driver, but I am an engineer and that just doubles my fun when driving on a closed course. It would not be a good idea to lend me your keys…
I have also had the privilege of driving on a NASCAR track at 165 mph. Remember a few paragraphs back when I told you about how inertia (centrifugal force) makes you feel like you are being pulled to the left or right in a curve? On a NASCAR track that same inertia makes you feel like someone is pushing on your shoulders as you are being squashed into your seat. Why? Superelevation.
On a superelevated (banked) curve we slope the pavement so that the major forces of friction, inertia, and gravity balance to the point that the vehicle gets pushed into the pavement on the curve rather than being forced to slide off the curve which would occur if the curve was flat. I’m struggling to not go into detail about the effects of temperature, tire condition, pavement condition, aero-dynamics, suspension, humidity, fuel load (and much more) on how fast a race car can go around a curve – but in racing, the devil is in the details, and those details involve a lot of engineering.
Our interstates are built the same way, but our superelevation factors have to consider a wide range of vehicles and weather conditions – though we definitely don’t design to 185 mph! Although I have been known to exceed the speed limit on occasion, the idiots that swerve through traffic at triple digit speeds are simply ignorant of the factors that affect their ability to get home safely:
- Their cars aren’t designed for that speed
- Their tires aren’t designed for that speed
- The roads aren’t designed for that speed
- The presence of debris, potholes and moisture can’t be predicted on a public road
- You (the idiot) might be the best driver to ever live. The driver of the other car that you are swerving around may not be…
Off the soapbox and back to the McSETT booklet and why “wet” and “icy” roads can become unsafe:
The concept is that icy roads are more slippery (lower friction factor) than dry roads and wet roads fall between the two. We have to design roads to be safe under each of these conditions. Speed is a factor as well. When a vehicle runs through the McSETT course sometimes it will fly off of a curve because it is traveling too fast for the superelevation (cross slope) of the curve and the low friction factors of the plastic track and hard plastic wheels. Sometimes the vehicle slides down on the curve because it is traveling too slowly. These issues occur in the real world as well and you can see grooved pavement, cross slopes and varying speed limits as part of the engineer’s design. This is the most obvious on interstate entrance and exit ramps.
Engineers also have to design for different vehicles. A semi-trailer truck has a high center of gravity making it prone to tipping over on curves. Passenger cars can drift through corners depending on the friction of the pavement, radius of the curve, and weight distribution of the vehicle.
The test track portion of the McSETT provides for discussion of “horizontal curves”, “vertical curves” and “super elevation” which allows the students to experiment with different vehicles, different track configurations, and different vehicle speeds to find the combination that allows each different model car to move through the course in the fastest and safest manner. The conversation with high school students, who may be driving and are therefore familiar with driving around curves when entering and leaving the highway, is more detailed. (Note: high schoolers like the model cars just as much as the younger kids!)
The students are then challenged to look around on the way home and whenever they are near a paved area to determine if it’s flat and think about why it never is truly “flat”.
I bet you will too!
Drive safely!

Howard
If you have a specific question, or a topic that you would like learn about, drop me a line at Engineer@HamiltonConsultingEngineers.com. Include “Ask an Engineer” in your subject line. I will respond.